Background
k-Nearest Neighbors (k-NN) is one of the simplest machine learning algorithms. k-NN is commonly used for regression and classification problems, which are both types of supervised learning. In regression, the output is continuous (e.g. numerical values, such as house price), while in classification the output is discrete (e.g. classifying cats vs. dogs).
To illustrate how the k-NN algorithm works, let’s consider a simple example of classifying whether a student will pass or fail a test given how many hours they slept and how many hours they studied. As shown in the figure below, hours slept is on the x-axis and hours studied is on the y-axis; our dataset has 3 examples where a student passed (blue points) and 3 examples where a student failed (red points). Our task is to classify the green student (4 hours slept, 5 hours studied).
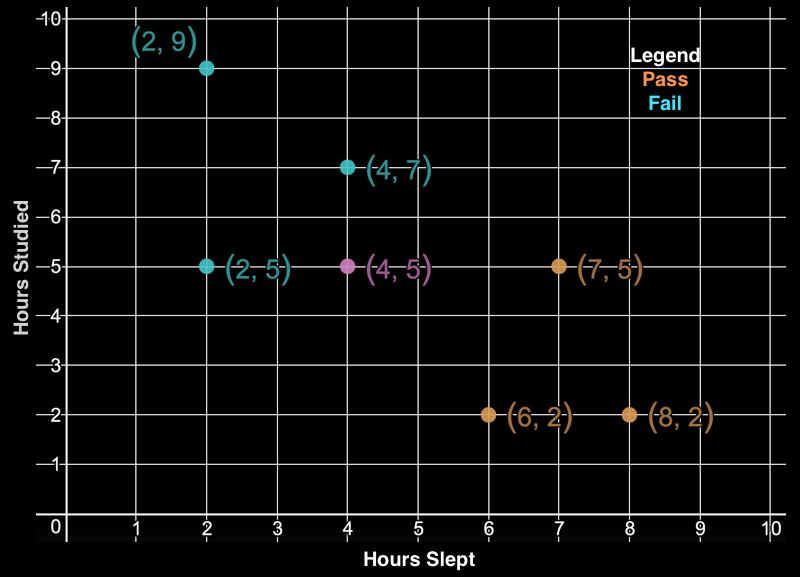
k-Nearest Neighbors Algorithm
In k-NN, \(k\) is a hyperparameter: a parameter of the model that is chosen ahead of time and that can be tweaked during successive trials to improve performance. The crux of the k-NN algorithm is to examine the \(k\) closest training examples to our test element. We measure closeness using feature similarity: how similar two elements are on the basis of their features.
In this example, our features are just hours slept and hours studied. We can measure how close the green student (our test element) is to the other example students using Euclidean distance. Recall that the Euclidean distance between two points \(p = (p_{1}, p_{2},...,p_{n})\) and \(q = (q_{1}, q_{2},...,q_{n})\) for n-dimensions is given by:
\[d(p,q) = d(q,p) = \sqrt{(p_{1} - q_{1})^2 + (p_{2} - q_{2})^2 + ... + (p_{n} - q_{n})^2}\]Therefore, we can use Euclidean distance to find the \(k\) closest example students to the green student. We will use \(k=3\) in this example.
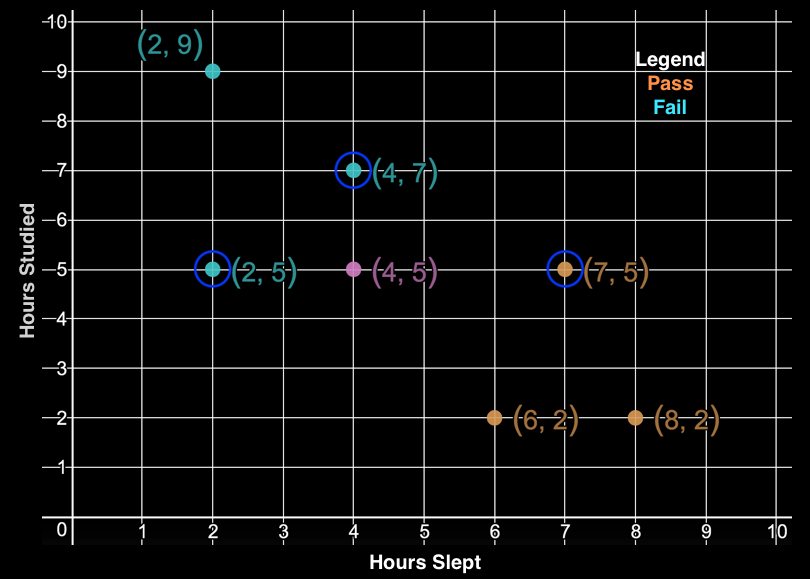
For classification, the k-NN algorithm outputs the class most common among its \(k\) nearest neighbors. Thus, because 2 of the 3 neighboring students we examined failed, we predict that the green student will fail as well. As an extension for regression problems, k-NN outputs the average of the values among its \(k\) nearest neighbors.
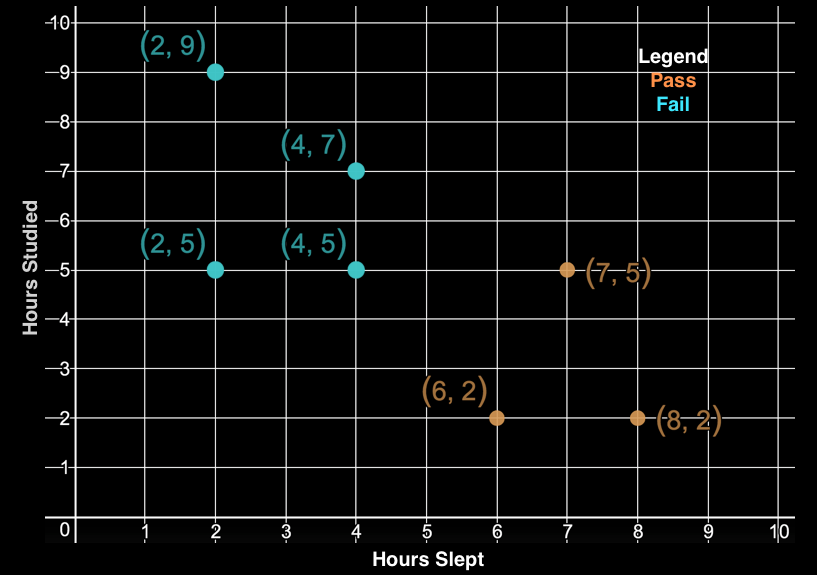
Choosing an appropriate value for \(k\) is critical for the algorithm’s performance and often depends on the number of training examples. A small value of k may cause the algorithm to be sensitive to noise in the dataset, while a large value may be computationally expensive.
To improve performance in cases where there is a skewed proportion of training examples per class, the distance of each neighbor is often weighted into the decision process. In addition, if features are not continuous variables, an overlap metric such as the Hamming distance can be used. Despite its simplicity, k-NN often works surprisingly well for many real-life examples.
Review Questions
-
k-NN uses...
A) Supervised Learning
B) Unsupervised Learning
C) Reinforcement Learning
D) Deep Learning
-
You have just trained a k-NN model on a dataset. Rather than using separate data for the testing phase, you decide to just re-use some of the training data. What will be the optimal value of k?
A) All values of k yield the same model accuracy
B) K = the number of classifications used
C) K = N
D) K = 1
Answers
-
k-NN uses...
A) Supervised Learning
B) Unsupervised Learning
C) Reinforcement Learning
D) Deep Learning
Training a k-NN model requires labeled training data. During testing, the model’s prediction is compared to the actual (labeled) answer. -
You have just trained a k-NN model on a dataset. Rather than using separate data for the testing phase, you decide to just re-use some of the training data. What will be the optimal value of k?
A) All values of k yield the same model accuracy
B) K = the number of classifications used
C) K = N
D) K = 1
Choosing k = 1 guarantees 100% accuracy. Every data point you test will fall directly on top of another point from the training set, namely the point itself. Picking a larger k no longer guarantees the testing point will receive the same classification as its copy from the training set, since nearby points will be considered as well.





